|
|
原文见:
http://www.cnblogs.com/atyuwen/archive/2010/09/12/coin.html
认为这篇文章有些可看的地方, 并且有些疑惑的地方,因此在 茶社发贴,
一是 可以和感兴趣的朋友讨论, 第二个目的是备份一份该资料,以便日后查看.
一个有趣的抛硬币问题 [blockquote]假设有一个硬币,抛出字(背面)和花(正面)的概率都是0.5,而且每次抛硬币与前次结果无关。现在做一个游戏,连续地抛这个硬币,直到连续出现两次字为止,问平均要抛多少次才能结束游戏?注意,一旦连续抛出两个“字”向上游戏就结束了,不用继续抛。
[/blockquote]上面这个题目我第一次见到是在pongba的TopLanguage的一次讨论上,提出问题的人为Shuo Chen,当时我给出了一个解法,自认为已经相当简单了,先来考虑一下抛硬币的过程:首先先抛一枚硬币,如果是花,那么需要重头开始;如果是字,那么再抛一枚硬币,新抛的这枚如果也是字,则游戏结束,如果是花,那么又需要重头开始。根据这个过程,设抛硬币的期望次数为T,可以得到关系
T = 1 + 0.5T + 0.5( 1 + 0.5 * 0 + 0.5T)
解方程可得到 T = 6. 由于上面这个方法只能得到期望,而无法得到方差以及具体某个事件的概率,后来我又仔细分析了一下,推出了概率生成函数为(推导的过程暂时略过,后面你会看到一个更一般、更简单的推导)
=\\\\frac{z^2}{4-2z-z^2})
于是可以算出方差 V = G''(1) + G'(1) - G'(1)^2 = 22。将G(z)根据Rational Expansion Theorem [CMath 7.3]展开,可以得到需要抛n次硬币的概率为
[img]http://latex.codecogs.com/gif.latex?[z^n]G(z)=\\frac{1}{2\\sqrt{5}}(\\frac{1+\\sqrt{5}}{4})^{n-1}-\\frac{1}{2\\sqrt{5}}(\\frac{1-\\sqrt{5}}{4})^{n-1}=\\frac{1}{2^n}F_{n-1}[/img]
其中Fn是Fibonacci数列的第n项。到这里,我觉得这个问题似乎已经完全解决了,直到昨天看到Matrix67的牛B帖。在此帖中Matrix67大牛用他那神一般的数学直觉一下将需要连续抛出n个字的一般情形给解决了,而且得出的结果相当简洁:Tn = 2^(n+1) - 2,其中Tn为首次出现连续的n个字的期望投掷数。这也给了我一些启发,我试着将上面的过程进行推广,居然得到一个简单得出人意料的解法(甚至比上面n=2的推导过程还简单)。这个解法的关键在于下面这个递推关系
Tn = Tn-1 + 1 + 0.5 * Tn
也即是有 Tn = 2 * Tn-1 + 2。由于 T1 = 2,因此可以得到 Tn = 2^(n+1) – 2。上面的递推关系是怎么来的呢,一个直观的理解是这样的:首先先抛掷Tn-1次,得到连续的n-1个字,然后再抛一次,若是字,则游戏结束;否则需要重头开始,也就是说又需要 Tn 次。
期望投掷次数已经得出来了,但是我们还想知道方差、恰好需要投掷 m 次的概率等其它一些更具体的性质。为了方便理解概率的分布情况,我先用程序生成了一个概率表如下所示。在下表中,第n行、第m列的元素为 Pnm,表示首次出现连续n个字的投掷数为m的概率。
| 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | 1/128 | 1/256 | 1/512 | 1/1024 | | 0 | 1/4 | 1/8 | 2/16 | 3/32 | 5/64 | 8/128 | 13/256 | 21/512 | 34/1024 | | 0 | 0 | 1/8 | 1/16 | 2/32 | 4/64 | 7/128 | 13/256 | 24/512 | 44/1024 | | 0 | 0 | 0 | 1/16 | 1/32 | 2/64 | 4/128 | 8/256 | 15/512 | 29/1024 | | 0 | 0 | 0 | 0 | 1/32 | 1/64 | 2/128 | 4/256 | 8/512 | 16/1024 |
仔细观察上表,你发现什么有趣的性质没?如果忽略掉分母的话,那么第n行恰好是一个n阶Fibonacci数列。例如可以考查各行的最后一列,有
[blockquote]第一行:1 = 1
第二行:34 = 21 + 13
第三行:44 = 24 + 13 + 7
第四行:29 = 15 + 8 + 4 + 2
第五行:16 = 8 + 4 + 2 + 1 + 1
[/blockquote]怎么解释这个现象呢?我们再来仔细考虑一下掷硬币的过程,为方便在下文中用1表示字,用0表示花,于是我们的目标是要恰好使用m次投掷,得到连续的n个1.
[blockquote]若第一次的结果为 0,那么剩下的任务就是恰好使用m-1次投掷得到到连续的n个1.
若前两次的结果为 10, 那么剩下的任务就是恰好使用m-2次投掷得到到连续的n个1.
若前三次的结果为 110, 那么剩下的任务就是恰好使用m-3次投掷得到到连续的n个1.
若前四次的结果为 1110, 那么剩下的任务就是恰好使用m-4次投掷得到到连续的n个1.
…
若前n-1次的结果为 1…10(n-2个1), 那么剩下的任务就是恰好使用1次投掷得到到连续的n个1.
[/blockquote]你或许已经看出来了,这里实际上是在枚举首次出现0的位置。由于首个0出现在位置i的概率为1/2^i,于是得到Pnm的递推公式
}+\\\\frac{1}{4}P_{n(m-2)}+\\\\frac{1}{8}P_{n(m-3)}+\\\\cdots)
于是根据初始条件: , , ,我们可以推出所有事件的概率。现在来推一下概率生成函数,设需要得到连续n个1的投掷数的概率生成函数为Gn(z),于是有 ,我们可以推出所有事件的概率。现在来推一下概率生成函数,设需要得到连续n个1的投掷数的概率生成函数为Gn(z),于是有
[url=http://www.codecogs.com/eqnedit.php?latex=G_n(z)=P_{n0}@plus _{n1}z@plus _{n1}z@plus _{n2}z^2@plus _{n2}z^2@plus _{n3}z^3@plus;\\cdots@plus _{n3}z^3@plus;\\cdots@plus _{nn}z^n@plus _{nn}z^n@plus _{n(n@plus;1)}z^{n@plus;1}@plus;\\cdots] _{n(n@plus;1)}z^{n@plus;1}@plus;\\cdots]=P_{n0}+P_{n1}z+P_{n2}z^2+P_{n3}z^3+\\\\cdots+P_{nn}z^n+P_{n(n+1)}z^{n+1}+\\\\cdots) [/url] [/url]
根据上面的递推公式和初始条件,可以得到
(1-\\\\frac{1}{2}z-\\\\frac{1}{4}z^2-\\\\cdots-\\\\frac{1}{2^n}z^n)=\\\\frac{1}{2^n}z^n)
于是可解得
=\\\\frac{z^n(2-z)}{2^{n+1}(1-z)+z^{n+1}})
分别代入 n = 1 和 n = 2 可以得到
=\\\\frac{z}{2-z}=\\\\frac{1}{2}z+\\\\frac{1}{4}z^2+\\\\frac{1}{8}z^3+\\\\cdots)
=\\\\frac{z^2}{4-2z-z^2}=\\\\frac{1}{4}z^2+\\\\frac{1}{8}z^3+\\\\frac{2}{16}z^3+\\\\cdots)
以我们前面得到的结果一致,这证明这个概率生成函数的确是正确的。有了生成函数后,我们又多了一种计算期望的方式
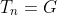
而方差也可以非常容易的得到
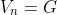
至此,这个抛硬币的问题终于应该算是被完全解决了,完。
我不明白 ,
(1)文中这个公式 T = 1 + 0.5T + 0.5( 1 + 0.5 * 0 + 0.5T) 是什么含义,如何理解?
(2)文中好几个公式出现的 Z 表示什么?.
|
|