|
|
楼主 |
发表于 2008-1-4 17:47:37
|
显示全部楼层
三等分任意角可能吗?
翻开报纸,往往有些科学新闻,是关于物理的、化学的、地球科学的等等,可曾看过有关数学的?绝无仅有!比起来,这些科学新闻的内容与生活较有关联,科学工作者比较容易告诉新闻传播者他们干了些什么,而新闻传播者也比较容易想象科学工作者做了些什么。(虽然有时候报导出来的不一定对)反观数学则不然,不但做的人没办法法说得清楚给外行人听,外行人也很难想象数学家们做了怎样的数学。结果数学新闻愈发死寂,而大家对数学也就愈加陌生。
纯数学的种种伟大发现或进展上周报吗?可能几十年来只有几件吧!最近的一次是前年夏天有关「四色问题」的解决(见《科月》65年12月及66年1月两期的〈四色足矣〉)。它之所以上报是因为一般人很容易懂它的内容。另外偶而会上报的是「某某人宣称解决了三等分任意角的难题」。虽然任意角不能三等分已成定案,而这类消息之所以上报是因为有很多非数学家都自以为很懂「三等分任意角」这个命题,因此有很多人拼命钻研这个号称是古希腊三大几何难题之一的做图题,也因此有很多人号称找到三等分任意角的方法,而且更有些编辑老爷也信以为真。很多人从小有大志,想成大名,于是从看起来简单的,所谓的几何三大难题下手。我在此为文的目的之一就是希望这些人能够平心静气看看一个学数学的谈数学界对这些问题的共同看法──它们是不可解的。希望我能说服这些人,不要把雄心壮志消磨在办不到的事情上。当然,我的更大的目的是要让《科月》的读者了解这些题目的本质,而对之有正确的看法。(我知道有中学老师鼓励学生钻研三大难题,谓解决其一即可得诺贝尔奖。)
三大难题
这三个题目是三分角、倍立方及圆化方,其内容分述如下。三分角:用直尺及圆规把任给的一角三等分。倍立方:给定一立方体(即其一边已知),用直尺及圆规做另一立方体(即做其一边)使其体积为原立方体的两倍。圆化方:用直尺及圆规做一正方形使其面积等于一给定圆的面积。
难题无解
这三个题目被研究了两千年,直到十九世纪代数学有了更进一步的发展后才有了答案。这个答案非常出人意表,即:只用直尺及圆规,这三个做图题都是无解的。所谓无解,就是说只用直尺及圆规我们没有办法把任意一角三等分等等。
许多人对「无解」的反应会是这样的:只是一时找不到适当的做图法吧!又没有把「所有」的方法一一试过,怎么就下结论说任何一种方法都不行?
玩过智慧盘吗?你一定知道有些排列没办法变成标准排列;同时你一定也知道 是不可能写成一个分数的。当然我们没有必要把「所有」的方法一一试过才下这种结论,我们另有方法证明这种不可能性。三大难题无解的证明也是一样的。
虽然数学家在十九世纪就证明了三大难题是无解的,但许多外行人,或许不知道无解的意义,或许没听过已经被证明为无解这件事,还是锲而不舍地钻研这些题目。其中尤其三分角最受人重视。本文主要要谈三分角,所以我们从三分角开始,例举一些他们可能犯的错误。
例一:設 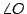 為給定的一角。以 O 為圓心,任意長 r 為半徑用圓規做圓,交 為給定的一角。以 O 為圓心,任意長 r 為半徑用圓規做圓,交 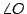 兩邊於 A,B(圖一)。不變圓規(即兩圓規腳之距離仍然保持 r 長),用兩圓規腳在直尺上刻劃兩點 C,D,則 CD 長為 r。用直尺,使 C 點保持在 BO 的延線上,D 點保持在圓上,調整直尺的位置,直到 A 點也在直尺上。做 兩邊於 A,B(圖一)。不變圓規(即兩圓規腳之距離仍然保持 r 長),用兩圓規腳在直尺上刻劃兩點 C,D,則 CD 長為 r。用直尺,使 C 點保持在 BO 的延線上,D 點保持在圓上,調整直尺的位置,直到 A 點也在直尺上。做 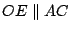 ,則 OE 為 ,則 OE 為 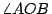 的三等分線之一。 的三等分線之一。
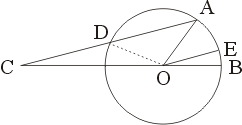
圖一 |
證明:聯 OD,則 CD=OD=OA=r,所以 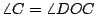 , , 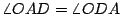 。由「三角形一外角等於其兩內角和」的定理知 。由「三角形一外角等於其兩內角和」的定理知 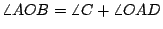 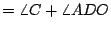 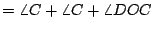 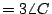 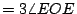 ,得證。 ,得證。
例一有什麼毛病?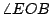 確實等於三分之一 確實等於三分之一 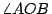 !但這種解法是違規的。原來所謂用直尺及圓規做圖是禁止在直尺上刻劃的。如果沒有這樣的規定,則三等分任意角,如例一所示,是可能的。 !但這種解法是違規的。原來所謂用直尺及圓規做圖是禁止在直尺上刻劃的。如果沒有這樣的規定,則三等分任意角,如例一所示,是可能的。
例二:設  為已知。以 O 為圓心,任意長 r 為半徑做弧交 為已知。以 O 為圓心,任意長 r 為半徑做弧交  兩邊於 A,B(圖二)。做 兩邊於 A,B(圖二)。做 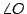 的平分線 OC。以 OC 為準線,B 為焦點做雙曲線 PQR 使曲線上任一點 R 到 B 的距離為到 OC 距離的兩倍。若雙曲線交弧於 Q,則 的平分線 OC。以 OC 為準線,B 為焦點做雙曲線 PQR 使曲線上任一點 R 到 B 的距離為到 OC 距離的兩倍。若雙曲線交弧於 Q,則  。 。
圖二 |
證明:聯 QB。做 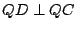 及 及 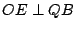 。因 。因 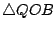 為等腰三角形,所以 OE 平分 為等腰三角形,所以 OE 平分 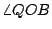 ,也平分 QB,故得 ,也平分 QB,故得 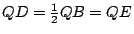 ,因此 ,因此 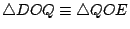 。由此可知 。由此可知 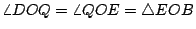 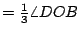 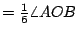 ,而得 ,而得 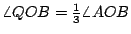 。 。
例二有什麼毛病?毛病出在用了輔助線 PQR。如果只用直尺及圓規,雙曲線 PQR 是做不出來的。
例三:給定一角 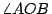 ,我們很容易把它二等分,四等分,八等分,……。做 ,我們很容易把它二等分,四等分,八等分,……。做 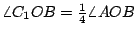 , , 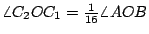 , , 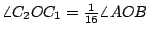 ,…, ,…, 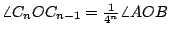 ,最後OC[sub]n[/sub]。會趨近一條定直線 OC,則 ,最後OC[sub]n[/sub]。會趨近一條定直線 OC,則  。(圖三) 。(圖三)
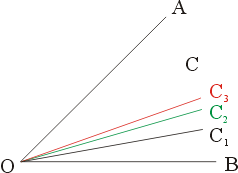
圖三 |
證明:
最後第二個等式由幾何級數的公式可得。例三又如何?理論上OC是存在的,但在有限步驟內是做不到的。幾何三大難題中所謂用直尺及圓規做圖是要求在有限步驟內完成的,所以例三又是個違規的例子。
以上三個例子雖然都違規,但到底都把三等分線做出來了。第四類的例子是根本沒把三等分線做出來,而居然用一些歪理證明做了三等分線。打個比方,籃球賽中常有進籃但因違規而被判無效的時候;而下面我們要舉的例子就像打霸王球,球都沒進籃而硬說進籃得分。
一般說來,業餘從事三等分角的人所犯的錯誤常屬於第四類。這一類的錯誤有的荒唐到極點,有的則論證非常複雜,但其中錯了一點(因此全盤盡沒)。在此只舉一個荒唐的例子。
例四:做兩條平行線。在其中的一直線上任取一點 D。以 D 為圓心,任意長r 為半徑做弧交此兩平行線於 F 及 C(圖四)。以 F 為圓心,r 為半徑做弧交下一直線於 B。按順序做 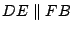 , , 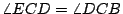 , ,  ,則 FD 及 CD 三等分 ,則 FD 及 CD 三等分 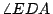 。 。

圖四 |
不錯,FD 及 CD 三等分了 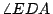 ;但天啊!在這個例子裏,我們先造了一個任意角 ;但天啊!在這個例子裏,我們先造了一個任意角 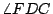 ,然後再做其三分之一角。這就像把牛車放在牛前而要牛拉著牛車走一樣的荒唐。 ,然後再做其三分之一角。這就像把牛車放在牛前而要牛拉著牛車走一樣的荒唐。
讀者千萬不要笑我舉了這樣的例子。事質上這個例子不是我杜撰的,這位將牛車放在牛前的人士還大有來頭──他是美國某大學的校長。他在1931年出版了兩本著作。第一本是長達三百多頁,名為《歐幾里得還是愛因斯坦》的巨作。他在這本書裡「證明」了平行公理(事實上,這又是一個無法證明的公理),而把研究非歐幾何學的人(包括愛因斯坦在內)臭罵一頓。第二本是《三等分一角》,他的做法就是我們的例四。這種唐吉訶德式研究數學的人士在每個地方,每個階層都有。
現在回過頭來談談只用直尺及圓規能做些什麼,還有,為什麼不能三等分一角。
直尺只能用來畫直線,直尺本身不能有任何刻度,像例一那樣是違規的,圓規只能用來畫圓。所有的曲線都要用直尺及圓規畫出,像例二那樣借用輔助曲線是不行的。此外,規定做圖都要在有限步驟內完成,像例三那樣就不算數。
用直尺及圓規每一步驟只能做下面三件事之一:(1)兩點間聯一直線,(2)以一點為圓心,一定長為半徑做圓,(3)取得兩直線,兩圓或一直線一圓間的交點。
一個做圖題總是有些已知的東西,譬如一些點、一些直線(或線段)、一些圓(或圓弧)。已知一線段的長度為已知,已知圓的圓心及半徑為已知。由這些已知的東西經由上述的步驟可以做出新的點、線、線段、圓或圓弧。這就是所謂的做圖題。
做圖題的要點之一就是要分析所要做的和已知之間的關係。這種關係最好是代數關係,因為有了代數關係比較容易知道怎麼去做圖。
為了研究幾何間的代數關係,我們最好引進解析幾何。在解析幾何中,我們用座標來表平面上的點,用一次方程式表直線,用二次方程式表圓,甚至三分角的問題也可以用代數式子來表示,這一點我們會慢慢談到。
在整個做圖課題中,最重要的是按分析由一線段 S 出發,我們能做出那些線段,由中學課本知,用直尺及圓規,我很容易做一線段使其長為 S 長的二倍、三倍、……、n 倍,我們也知道如何把一線段等分、三等分、……、m等分。因此也能做出一線段使其長為 S 長的 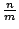 倍,即 S 長的任何正分數倍都可以做出來。如果用解析幾何的觀點──線段的長短加上方向──則 S 長的任何有理數倍長的線段都可以做出來。 倍,即 S 長的任何正分數倍都可以做出來。如果用解析幾何的觀點──線段的長短加上方向──則 S 長的任何有理數倍長的線段都可以做出來。
為了方便行文起見,我們可以用 S 的長度做為座標系統中的單位長,則 S 對應到座標系統中的 1。由上述的討論知任何有理數系統中的元素都可以做出來。(即可以做出長度為 S 長的該有理數倍的線段)
當然,可以做出來的不只是有理數。譬如,假定一正實數 a 是可做的,則 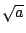 也可以做其做法如下:(圖五)用 a+1 的長度為直徑做半圓,在 B 點立 AC 的垂直線,交半圓於 D,則 BD 的長度為 也可以做其做法如下:(圖五)用 a+1 的長度為直徑做半圓,在 B 點立 AC 的垂直線,交半圓於 D,則 BD 的長度為 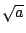 。(可由兩直角三角形 ABD 及 DBC 之相似證得) 。(可由兩直角三角形 ABD 及 DBC 之相似證得)
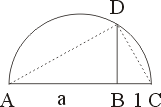
圖五 |
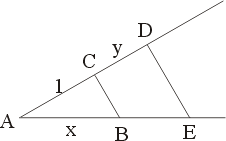
舉個特例,有理數2是可做的,所以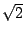 也可做。更有進者, 也可做。更有進者,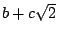 (b,c都是有理數)這種形式的數都可做。我們當然可以用 (b,c都是有理數)這種形式的數都可做。我們當然可以用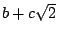 這類數為a而做出更複雜的數 這類數為a而做出更複雜的數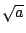 (即 (即 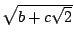 等等。 為了區別這些做出的數的繁簡程度,我們要定義 n 階數。假設a,b,c是有理數而a>0,則稱 等等。 為了區別這些做出的數的繁簡程度,我們要定義 n 階數。假設a,b,c是有理數而a>0,則稱 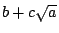 這樣的數為1階可做數,簡稱1階數。因為我們可以取c=0,所以1階數包括有理數。當 a[sub]1[/sub]=a[sub]2[/sub] 時,兩個1階數 這樣的數為1階可做數,簡稱1階數。因為我們可以取c=0,所以1階數包括有理數。當 a[sub]1[/sub]=a[sub]2[/sub] 時,兩個1階數 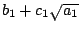 及 及  稱為同類的一階數。有了1階數及其同類關係,我們可以定義2階數,即 稱為同類的一階數。有了1階數及其同類關係,我們可以定義2階數,即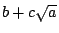 ,其中 a,b,c 都是同類的1階數而a>0。這些2階數都是可做的,這是因為 ,其中 a,b,c 都是同類的1階數而a>0。這些2階數都是可做的,這是因為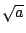 ,b,c都是可做數,而可做數相加還是可做數,可做數相乘還是可做數。後者的證明如下:設x,y為可做數。(圖六)做兩條相交的直線,其交點為A。在一直線上取AB,使其長為x。在另一直線上取單位長AC,再取CD,使其長為y。聯CB,做 ,b,c都是可做數,而可做數相加還是可做數,可做數相乘還是可做數。後者的證明如下:設x,y為可做數。(圖六)做兩條相交的直線,其交點為A。在一直線上取AB,使其長為x。在另一直線上取單位長AC,再取CD,使其長為y。聯CB,做  ,交AB於E。由比例關係知BE長為xy。 ,交AB於E。由比例關係知BE長為xy。
圖六 |
若將1和x對調,則BE長為 ,可見可做數相除仍為可做數。因此可做數相加、減、乘、除仍為可做數。用現代的術語來說,若一個數集中的任兩元素互相加減乘除後仍然在該數集中,則此數集稱為一個「體」。我們知道有理數集是一個體,實數集是一個 一個體,而可做數集也是一個體。 ,可見可做數相除仍為可做數。因此可做數相加、減、乘、除仍為可做數。用現代的術語來說,若一個數集中的任兩元素互相加減乘除後仍然在該數集中,則此數集稱為一個「體」。我們知道有理數集是一個體,實數集是一個 一個體,而可做數集也是一個體。
我們可以按順序定義 3 階數,4 階數,…,及同階數間的同類關係。假設 n-1 階數及其同類關係已經定義過,則 n 階數呈 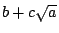 形式,其中a,b,c 是同類的 n-1 階數,而 a>0。若 a[sub]1[/sub]=a[sub]2[/sub],則兩 n 階數 形式,其中a,b,c 是同類的 n-1 階數,而 a>0。若 a[sub]1[/sub]=a[sub]2[/sub],則兩 n 階數 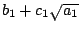 , ,  稱為同類。同類的 n 階數組成一個體,其證明由合用歸納法及根式有理化法可得。一個 n 階數可以看或一個階數比 n 高的數;一個 n 階數有時也同時可能是一個階數比 n 為低的數;如果一個 n 階數不能同時也是個階數較低的數,則稱為純 n 階數。所有的階數,1 階數,…,n 階數,都叫做可做數。 稱為同類。同類的 n 階數組成一個體,其證明由合用歸納法及根式有理化法可得。一個 n 階數可以看或一個階數比 n 高的數;一個 n 階數有時也同時可能是一個階數比 n 為低的數;如果一個 n 階數不能同時也是個階數較低的數,則稱為純 n 階數。所有的階數,1 階數,…,n 階數,都叫做可做數。
例五: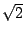 和 和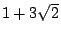 是同類的1階數, 是同類的1階數,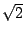 和 和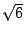 為不同類的1階數, 為不同類的1階數, 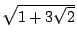 和 和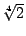 為不同類的2階數;。 為不同類的2階數;。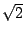 也可以看成2階數(因為 也可以看成2階數(因為 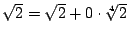 ), ),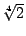 是純2階數, 是純2階數,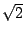 則不然。 則不然。
綜上所述,由一線段S出發,我們可以做出可做數倍長的線段。
反過來,我們要證明由一線段S出發,用直尺及圓規只能做出這些可做數倍長的線段。
現用歸納法證明如下。一直線可以其上的兩點表出,一圓可以其圓心及半徑長表出,而半徑長或線段長可以兩點之間的距離表出(譬如,這兩點可以是平面上的座標原點和實軸上距原點為該長度的點)。用直尺及圓規在n步驟內我們得到了一些點、一些直線、一些線段、一些圓。假定這些點及代表直線、線段及圓的點的座標都是同類的n階數,我們要證明到下一步驟已做出的點其座標都是同類的 n+1 階數。(若座標可做則點可做,反之亦然。)
若第 n+1 步驟做的是聯結兩已做點而做直線或是以已做點為圓心,已做長為半徑做圓,則我們並沒有得到新的(代表)點。如果聯結兩已做點 (x[sub]1[/sub],y[sub]1[/sub]),(x[sub]2[/sub],y[sub]2[/sub]) 而得這兩點間的線段,則此線段長為  。它是個 n+1 階數,且和原有的點的座標(看成 n+1 階數)同類。 。它是個 n+1 階數,且和原有的點的座標(看成 n+1 階數)同類。
另一能得到新點的是做兩已做直線,兩已做圓或一已做直線,一已做圓之間的交點。設兩直線分別通過 (x[sub]1[/sub],y[sub]1[/sub]),(x[sub]2[/sub],y[sub]2[/sub]) 及 (x[sub]3[/sub],y[sub]3[/sub]),(x[sub]4[/sub],y[sub]4[/sub]),則其方程式分別為 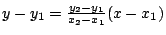 及 及 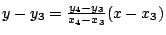 ,而得其交點的座標為 x[sub]i[/sub],y[sub]j[/sub]( ,而得其交點的座標為 x[sub]i[/sub],y[sub]j[/sub](  )的有理函數,所以新點的座標仍為同類的 n 階數。 )的有理函數,所以新點的座標仍為同類的 n 階數。
設兩圓的圓心分別為 (x[sub]1[/sub],y[sub]1[/sub]),(x[sub]2[/sub],y[sub]2[/sub]),半徑長分別為 r[sub]1[/sub],r[sub]2[/sub],則其方程式分別為 (x-x[sub]1[/sub])[sup]2[/sup]+(y-y[sub]1[/sub])[sup]2[/sup]=r[sub]1[/sub][sup]2[/sup] 及 (x-x[sub]2[/sub])[sup]2[/sup]+(y-y[sub]2[/sub])[sup]2[/sup] = r[sub]2[/sub][sup]2[/sup]。兩式相減,x[sup]2[/sup],y[sup]2[/sup] 項消去,可得 x 及 y 的一次式。以之代回兩式之一,可得 x 的二次方程式。由此知交點的橫座標 x 呈 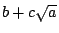 形式。其中 a,b,c 全為 x[sub]1[/sub],x[sub]2[/sub],y[sub]1[/sub],y[sub]2[/sub],r[sub]1[/sub],r[sub]2[/sub] 的有理函數。所以 x 為 n+1 階數。因 y 與 x 有線性(即一次)關係,所以 y 也是 n+1 階數,且和 x 同類。更有進者,x,y 和原有點的座標(看成 n+1階數)都同類。同樣的證法可以用來處理一圓及一直線相交的情形。 形式。其中 a,b,c 全為 x[sub]1[/sub],x[sub]2[/sub],y[sub]1[/sub],y[sub]2[/sub],r[sub]1[/sub],r[sub]2[/sub] 的有理函數。所以 x 為 n+1 階數。因 y 與 x 有線性(即一次)關係,所以 y 也是 n+1 階數,且和 x 同類。更有進者,x,y 和原有點的座標(看成 n+1階數)都同類。同樣的證法可以用來處理一圓及一直線相交的情形。
這樣,我們用歸納法證明了在 n 步驟內做出的點的座標為 n 階數。也就是說在有限步驟內我們能做的是可做數。簡單地說,可做的數可以用 +,-,×, , , 及整數表出。 及整數表出。
有一點須要說明:在做圖過程中,我們常「任取一點」、「任做一直線」或「任做一圓」。由此所得點及線、圓的代表點的座標當然不一定是可做數。但既然是「任取」或「任做」,這表示最後所得結果與取那一個或做那一個無關。所以我們可以取一點、做一直線或做一圓使其代表點的座標為已做出的數。因為有理數為 0 階數,且在實數系統中密集,所以我們可以假定這些座標為 0 階數。有了這樣的說明,我們的證明就不是以偏概全了。
另一點值得注意的是:一直線 ax+by+c=0 或一圓 x[sup]2[/sup]+y[sup]2[/sup]+ax+by+c=0 是否可做,全決定於 a,b,c 是否都可做。
經過這樣的分析後,我們可以證明三等分任意角的不可能性了。其要點有二,一為:不是任何實數都是可做數,一為:假定一角可以三等分,則某個線段長 x 為可做,但由代數的分析又知 x 不為任何 n 階數,故得矛盾。
詳細的討論如下:設  為給定的一角。假定用直尺及圓規可以將 為給定的一角。假定用直尺及圓規可以將  三等分,即可以做直線 OT 而有如圖七所示的關係。今在 三等分,即可以做直線 OT 而有如圖七所示的關係。今在  的一邊上任取一點 A,以 O 為圓心,OA 為半徑做弧交 的一邊上任取一點 A,以 O 為圓心,OA 為半徑做弧交  的另一邊於 B,交 OT 於 C。做 的另一邊於 B,交 OT 於 C。做 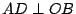 , ,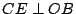 。我們可以假定 OA 的長度為單位長。(其他線段的長度則由與 OA 相比而得)令 OD 長為 a,OE 長為 x(即 OD 長為 OA 長的 a 倍,OE 長為 OA 長的 x 倍)。則 。我們可以假定 OA 的長度為單位長。(其他線段的長度則由與 OA 相比而得)令 OD 長為 a,OE 長為 x(即 OD 長為 OA 長的 a 倍,OE 長為 OA 長的 x 倍)。則 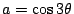 , ,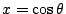 。由 。由 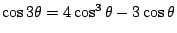 ,則得 a=4x[sup]3[/sup]-3x。由此可知,如果 ,則得 a=4x[sup]3[/sup]-3x。由此可知,如果 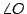 可以三等分,則由線段 OA 出發,x 是可做的,而且滿足上述的關係。但對某些 a 來說,這是一種矛盾。為此,我們證明一個比較廣泛的定理。 可以三等分,則由線段 OA 出發,x 是可做的,而且滿足上述的關係。但對某些 a 來說,這是一種矛盾。為此,我們證明一個比較廣泛的定理。
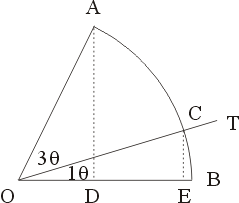
圖七 |
定理一:若有理係數方程式 ax[sup]3[/sup]+bx[sup]2[/sup]+cx+d=0 為不可約(在有理數中),則其三根皆為不可做。
證明:若不然,設 x[sub]1[/sub] 為可做根中純階數最低的一根。設其純階數為 n。則  ,而 e,f,h 為同類的 n-1 階數, ,而 e,f,h 為同類的 n-1 階數, ,h>0。且非某 n-1 階數的平方數。我們假定 ,h>0。且非某 n-1 階數的平方數。我們假定  ,否則 x[sub]1[/sub] 為有理數,而方程式就因有有理根而變成可約了。 ,否則 x[sub]1[/sub] 為有理數,而方程式就因有有理根而變成可約了。
將 x[sub]1[/sub] 代入方程式中,經整理後得  ,其中 ,其中
由於 s,t 都是 n-1 階數,而 h 不是任何 n-1 階數的平方,所以由 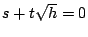 可得 s=t=0。若令 可得 s=t=0。若令 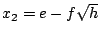 ,以之代入方程式則得 ,以之代入方程式則得 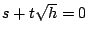 。所以 x[sub]2[/sub] 也是方程式的一根。今假定 x[sub]3[/sub] 為方程式的第三根,則由根與係數的關係,得 。所以 x[sub]2[/sub] 也是方程式的一根。今假定 x[sub]3[/sub] 為方程式的第三根,則由根與係數的關係,得 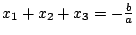 ,即 ,即 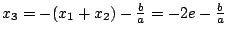 。則 x[sub]3[/sub] 為 n-1 階數。此與對 n 之假定矛盾,故得定理。 。則 x[sub]3[/sub] 為 n-1 階數。此與對 n 之假定矛盾,故得定理。
一有理係數方程式若可約,則必有一次的有理係數因式,因此有一有理根。所以為了應用定理一,我們要知道一個有理係數多項式何時有有理根。關於此,我們從中學數學課本知有
定理二:一整係數多項式 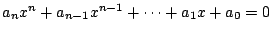 若有有理根,則此有理根必為 若有有理根,則此有理根必為 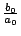 ,其中 b[sub]0[/sub],b[sub]n[/sub] 分別為 a[sub]0[/sub],a[sub]n[/sub] 的因子。 ,其中 b[sub]0[/sub],b[sub]n[/sub] 分別為 a[sub]0[/sub],a[sub]n[/sub] 的因子。
現在我們可以證明用直尺及圓規三等分任意角是不可能的。設  為 60°,則 為 60°,則 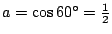 ,所以相對應的方程式為 ,所以相對應的方程式為 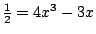 或 8x[sup]3[/sup]-6x-1=0。根據定理二,若此方程式有有理根,則此根必為 或 8x[sup]3[/sup]-6x-1=0。根據定理二,若此方程式有有理根,則此根必為  , , 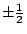 , , 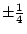 , , 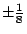 之一。但把這些數代入方程式知它們都不是根。所以原方程式沒有有理根,因此不可約,而根據定理一,則 x 為不可做。 之一。但把這些數代入方程式知它們都不是根。所以原方程式沒有有理根,因此不可約,而根據定理一,則 x 為不可做。
不但 60°不能用直尺及圓規三等分,還有許許多多的角也不能。反之,有些特殊角是可以三等分的。譬如大家都知道直角是可以三等分的,此外 45°也可以三等分,因為 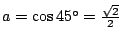 ,所以方程式為 ,所以方程式為 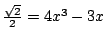 (它不是有理係數方程式)。但此方程式的三根分別為 (它不是有理係數方程式)。但此方程式的三根分別為 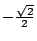 , , 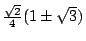 ,全是可做數。(事實上,x 為正,所以 ,全是可做數。(事實上,x 為正,所以 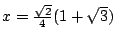 )。當然,我們可以先將 90°角三等分得 30°角,再把後者等分而得 15°角,此即 45°角的三分之一角。 )。當然,我們可以先將 90°角三等分得 30°角,再把後者等分而得 15°角,此即 45°角的三分之一角。
根據定理一、二,我們可以舉出許許多多不可用直尺及圓規三等分的角。不但如此,借用這兩個定理,我們可以輕易地證明倍立方一樣是不可能的。若原立方的邊長為 1,而 x 為所要的新立方的一邊,則 x[sup]3[/sup]-2=0。由定理一、二可知這樣的 x 是不可做。
至於圓化方的問題就比較複雜。首先,我們有比定理一更廣泛的定理。
定理三:x 為可做的一個必要條件是 x 為某 2[sup]m[/sup] 次有理係數多項式的根。
我們不想在此證明這個定理。我們只舉一個特殊例子,希望讀者由此大約可以想見一般的情形是怎麼證的。譬如 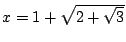 個2階數。移項得 個2階數。移項得 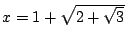 。平方得 。平方得 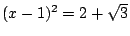 。移項得 。移項得 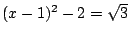 。平方得 ((x-1)[sup]2[/sup]-2)[sup]2[/sup]=3,整理得 x[sup]4[/sup]-4x[sup]3[/sup]+2x[sup]2[/sup]+4x-2=0。所以x為一有理係數四次方程式的根。一般說來,若x是m階數.則x為一2[sup]m[/sup]次有理係數方程式的根。 。平方得 ((x-1)[sup]2[/sup]-2)[sup]2[/sup]=3,整理得 x[sup]4[/sup]-4x[sup]3[/sup]+2x[sup]2[/sup]+4x-2=0。所以x為一有理係數四次方程式的根。一般說來,若x是m階數.則x為一2[sup]m[/sup]次有理係數方程式的根。
設圓的半徑長為1,則其面積為圓周率 π。若能圓化方,設 x 為正方形的一邊,則 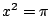 。若 x 可做,則它的平方 π 也可做,因此根據定理三,π 要為某 2[sup]m[/sup] 次有理係數多項式的根。自古以來,大家對於 π 是否為某一有理係數多項式的根的問題極感興趣。用現代的術語來說,一個有理係數多項式的根稱為代數數,否則為超越數。有理數是代數數;根據定理三,可做數都是代數數。那麼 π 是代數數嗎?1882年,德國數學家林德曼(F. Lindemann)證明了 π 不是代數數而是超越數,因此不可能是可做數。第三大難題也是不可解。 。若 x 可做,則它的平方 π 也可做,因此根據定理三,π 要為某 2[sup]m[/sup] 次有理係數多項式的根。自古以來,大家對於 π 是否為某一有理係數多項式的根的問題極感興趣。用現代的術語來說,一個有理係數多項式的根稱為代數數,否則為超越數。有理數是代數數;根據定理三,可做數都是代數數。那麼 π 是代數數嗎?1882年,德國數學家林德曼(F. Lindemann)證明了 π 不是代數數而是超越數,因此不可能是可做數。第三大難題也是不可解。
三大難題到1882年就全被證明為不可解了。百年之後還有人傻乎乎地要證其可解,能不令人搖頭嘆息?
讀者也許不服氣,問道:「為什麼要把直尺及圓規的使用限定得那麼死?用其他的規定來三等分一角不是也很好嗎?」不錯,用其他的規定也不壞。但數學的基本精神是先有了規定,才根據規定來談如何解問題或談問題是否可解。所謂三大難題,工具的使用規定就是那麼死,如果規定改了,則變成其他問題,再也不是所謂的三大難題了。就像玩象棋,規定象不能過河;若規定可以飛象過河,則成了另一種遊戲了。另一種遊戲好不好?只要有趣就值得玩玩。那麼三等分一角呢?從古以來就不斷有人改變規定,如用輔助工具(如例一,有刻度的直尺可視為輔助工具。),用輔助曲線(加例二)或使用趨近法(如例三)等。用新規定所得的數學知識及對其他數學的貢獻也不少,但就是因為原先死硬規定的題目最難、所以使人努力了兩千年之久。如果只用圓規或只用直尺如何?這方面也早有人研究過,也早就成定案。若只用圓規,意大利數學家馬歇羅尼(Mascheroni, 1750~1800)有個令人難以置信的答案:凡用直尺及圓規能做的,只用圓規也能做。(圓規當然不能畫直線;我們說圓規能做直線意即能做該直線上的兩點。)只用直尺呢?當然只用直尺,由單位長出發只能做出單位長的有理倍數長的線段,但德國數學家史坦納(J. Steiner, 1796~1863)卻有如下的定理:給定一個圓,則只用直尺可做出任何用直尺及圓規可做出的線段。換句話說,若圓規與直尺合用,圓規只用一次就夠了。
本文所談可做數的觀念也可以用來談論其他的做圖問題,如等分圓等。由於篇幅所限只能點到為止。
一般的做圖討論(包括三大難題、等分圓等)可參考 Courant 及 Robinson 合著的《數學是什麼》(what is mathematics) 一書。關於輔助曲線、輔助工具及趨近法,R. Yates 的書《三分角問題》(The trisection problem) 有非常精彩而且詳盡的討論。
註一:《數學是什麼》一書國內有兩種譯本出售。以水牛出版社用《數學導論》做書名吳定遠譯的較佳。 註二:商務人人文庫(561)《幾何三大問題》。
http://episte.math.ntu.edu.tw/articles/sm/sm_09_04_1/index.html |
|